AVO
Categories:
Description
These External Attribute scripts calculate various AVO related seismic attributes.
| SCRIPT | DESCRIPTION |
|---|---|
| ex_avoig_angle3.py | Compute intercept and gradient from 3 angle stacks. |
| ex_avoig_angle4.py | Compute intercept and gradient from 4 angle stacks. |
| ex_avoiig_angle5.py | Compute intercept and gradient from 5 angle stacks. |
| ex_fatti3_angle3.py | Compute Fatti 3 term reflectivity from 3 angle stacks. |
| ex_fatti3_angle4.py | Compute Fatti 3 term reflectivity from 4 angle stacks. |
Intercept and Gradient
Script: AVO/ex_avoig_angle3.py
Script: AVO/ex_avoig_angle4.py
Script: AVO/ex_avoig_angle5.py
Takes as input angle stacks and the corresponding angles and computes the Intercept \(\left(I\right)\) and Gradient \(\left(G\right)\) at each sample point as per Shuey’s 2 term approximation to the Aki-Richards equation:
$$ R(\theta) = I + G \sin ^{2}(\theta). $$
Possible outputs are the intercept, gradient and the quality or coefficient of determination \(\left(0\le R^2 \le 1 \right)\) of the linear fit.
Input Parameters
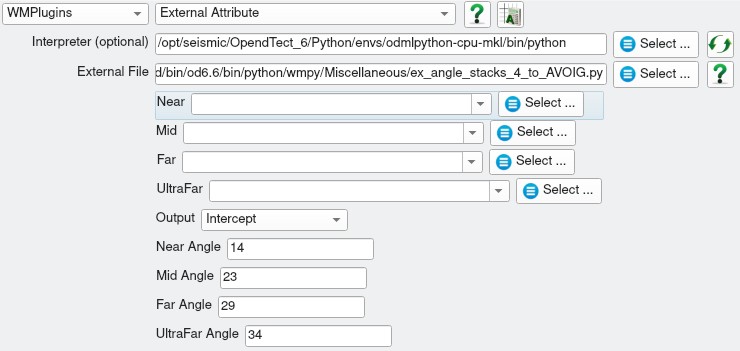
ex_avoig_angle4.py input parameters
For each input volume the corresponding incident angle must be provided.
AVO Fatti 3 Term
Script: AVO/ex_fatti3_angle3.py
Script: AVO/ex_fatti3_angle4.py
Takes as input angle stacks and the corresponding angles and computes the P-wave reflectivity \(\left(R_{P}\right)\), S-wave reflectivity \(\left(R_{S}\right)\) and Density reflectivity \(\left(R_{D}\right)\) at each sample point as per Fatti’s 3 term approximation to the Aki-Richards equation:
$$ R(\theta)=\left(1+\tan ^{2}\theta \right)R_{P}-\left(8{\frac {\beta ^{2}}{\alpha ^{2}}}\sin ^{2}\theta\right) R_{S}-\left(\tan ^{2}\theta -4{\frac {\beta ^{2}}{\alpha ^{2}}}\sin ^{2}\theta \right)R_{D}. $$
where
$$ R_{P} = {\frac {\Delta I_{P}}{2I_{P}}} = {\frac {\rho_{i}\alpha_{i} - \rho_{i-1}\alpha_{i-1}}{\rho_{i}\alpha_{i} + \rho_{i-1}\alpha_{i-1}}} $$ $$ R_{S} = {\frac {\Delta I_{S}}{2I_{S}}} = {\frac {\rho_{i}\beta_{i} - \rho_{i-1}\beta_{i-1}}{\rho_{i}\beta_{i} + \rho_{i-1}\beta_{i-1}}} $$ $$ R_{D} = {\frac {\Delta \rho }{2\rho }} = {\frac {\rho_{i} - \rho_{i-1}}{\rho_{i} + \rho_{i-1}}}$$ $$ {\frac {\alpha}{\beta}} = average V_{p} V_{s} ratio $$
and \(\alpha_{i}\) is the P-wave velocity, \(\beta_{i}\) is the S-wave velocity and \(\rho_{i}\) is the density of layer \(i\).
The script variants with 4 or more angle stack inputs also have the quality or coefficient of determination \(\left(0\le R^2 \le 1 \right)\) of the fit as a possible output.
Input Parameters

ex_fatti3_angle4.py input parameters
Feedback
Was this page helpful?
Glad to hear it! Please tell us how we can improve.
Sorry to hear that. Please tell us how we can improve.